Simple but effective time-series model forecasts the next 10 days of the pandemic in Morocco. As we come to grips with this hapless ‘new normal’, the pandemic shows no sign of abating; in fact, we should brace ourselves, for the worst is yet to come!

Introduction:
130 days ago, COVID-19 landed on Moroccan soil. Ever since, COVID-19 has been a force to be reckoned with. Merciless and insidious, the pandemic has inflicted its wrath on a defenceless populace. In its foray through the population, it visits homes, local communities and souqs uninvited and only departs after claiming lives. As it encroaches all facets of life: arts and sports; culture and society; and economy and politics, it leaves an indelible mark on Moroccan minds and the nation’s soul. In response, the government consigned its population to a lockdown on March 20th and an extension upon extension since April 18th, all but providing COVID-19 with the much-needed respite as it lurks in the shadows. Amid the pandemic raging on, Moroccans are compelled to embrace the ‘new normal’ within the confines of loosened lockdowns (1) and demarcated zones by epidemiological context (2,3). All of this begs the insoluble question: how long will this last? Frankly, only time will tell. Yet, more practically, we can ask what does the near future bode for Morocco (well, the next 10 days) in terms of cumulative cases and deaths and recoveries?

Methods:
Auto ARIMA: best model, stationarity and accuracy
I ran a 10-day projection on the cumulative cases, deaths and recoveries. I relied on the automatic Auto Regressive Integrated Moving Average (ARIMA) package in R to perform predictive modelling. ARIMA fits each model to a time-series data for a defined period at the 95% Confidence Interval. This technique is relatively novel in epidemic analysis, with studies in Italy (4,5) illustrating promising and accurate forecasts. I relied on the automated algorithm in R to fit the best ARIMA model for the transformed time-series data, hence automatic ARIMA*. The output produces a mean average prediction error (MAPE) in which I can ascertain the forecasts’ accuracy by this simple equation:

Accuracy (%) = 100% – MAPE (%)

*See statistical analysis for standard ARIMA specification

Results:
Forecasting cases, deaths and recoveries

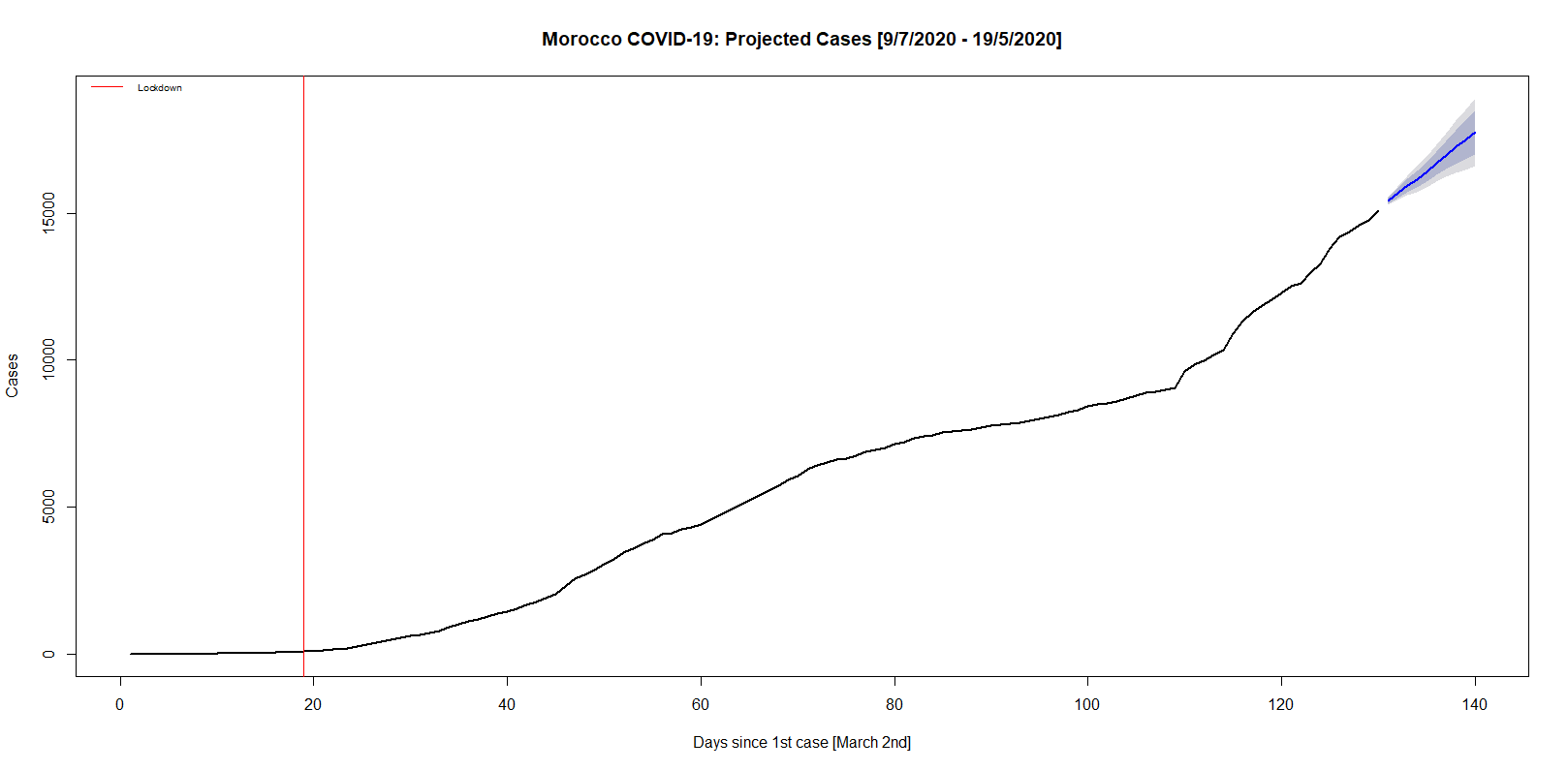
Graph 1: Projected cumulative cases from July 9th to July 19th

Graph 2: Projected deaths from July 9th to July 19th

Graph 3: Projected recoveries from July 9th to July 19th

I modelled the projected cases, deaths and recoveries for the next 10 days: from July 9th to June 19th, or, conveniently, day 130 to day 140 since first reported case on March 2nd (graphs 1-3). The projections show the three states are expected to stay on their respective trajectories. By July 19th, there is expected to be 2678 more cases, reaching a total of 17757 cases (95% CI: 16600-18913). Concurrently, there would be 16 deaths, which is equivalent to less than 2 deaths a day. Overall, the death toll would be 258 (95% CI: 227-289). Likewise, the number of people recovering are expected to rise by 1626 from 11477 to 13073 (95% CI: 11610-14536). All forecasts were validated with an accuracy of 96.63% (cases), 95.26% (deaths) and 93.94% (recoveries) in predicting the next 10 days. Whereas the latter’s lower relative accuracy is reflected by the abrupt spikiness of the trend, the death’s wider 95% confidence intervals with the lower interval being less than the actual death toll does pose empirical concerns. Nonetheless, one can deduce with confidence a steady increase in all states.

Concerns and scope:
ARIMA models provide a rough sketch of what to expect in the near future. Contingent on the data available, ARIMA is a simple but powerful tool. Inherently – and perhaps cynically – ARIMA models don’t change the overall trend; rather, they provide a short-term continuity to the trend. This is because ARIMA reviews the available data of dependent variables, i.e.: reported cases and deaths (8). According to ARIMA, everything operates in an intransigent linearity — fluctuations or the peak are hard to determine. In other words, ARIMA tells us what to expect without considering the implication on the overall trajectory.

Life is complex! We need a model that considers or is responsive to lockdown interventions and can be calibrated to the available data. The best way to go around this is to adopt a stochastic, Bayesian approach. Naturally, there are a lot of initial assumptions (priors) made on the future with relative uncertainty which can be updated throughout time (posteriors) to account for changes in policy or even behaviour. ARIMA needs to be taken with a pinch of salt and, at best, gives an informal summary of the short-term trajectory.

Nonetheless, the message is clear: cases and deaths are expected to increase in the short-term. There is good news: the simultaneous increase in recoveries will offset the deaths. But, more tellingly, there is bad news: COVID-19 is here to stay and we will have to live — willingly or reluctantly — with the pandemic’s pandemonium.

Statistical analysis for standard ARIMA:
Fitting the best model requires stationarity – an inherent assumption for ARIMA models. We ran a formal hypothesis test called the Augmented Dickey-Fuller (ADF) test for the three states, setting the significance level at 5%. Initially, the test for all models failed to reject the null hypothesis of non-stationarity (cases: p=0.651; deaths: p=0.648; recoveries: 0.778). Studies have rectified this issue by differencing (6,7), taking the difference between consecutive observations (or data-points) to stabilise the mean and variance over time. This process continued until the ADF rejects the null hypothesis of stationarity, where all the models had p=0.01.

References:

1. Kasraoui S. Govt. Clarification: Morocco Extends State of Emergency to July 10, Eases Lockdown [Internet]. Morocco World News. 2020 [cited 2020 Jun 10]. Available from: https://www.moroccoworldnews.com/2020/06/305307/govt-clarification-morocco-extends-state-of-emergency-to-july-10-eases-lockdown/
2. Kasraoui S. What You Need to Know About the 1st Phase of Morocco’s Lockdown Exit [Internet]. Morocco World News. 2020 [cited 2020 Jun 10]. Available from: https://www.moroccoworldnews.com/2020/06/305346/what-you-need-to-know-about-the-1st-phase-of-moroccos-lockdown-exit/
3. Guerraoui S. Morocco set to further ease coronavirus lockdown [Internet]. MEO. 2020 [cited 2020 Jun 10]. Available from: https://middle-east-online.com/en/morocco-set-further-ease-coronavirus-lockdown
4. Chintalapudi N, Battineni G, Amenta F. COVID-19 virus outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: A data driven model approach. Journal of Microbiology, Immunology and Infection [Internet]. 2020 Apr 13 [cited 2020 Apr 22]; Available from: http://www.sciencedirect.com/science/article/pii/S1684118220300980
5. Benvenuto D, Giovanetti M, Vassallo L, Angeletti S, Ciccozzi M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data in Brief. 2020 Apr 1;29:105340.
6. Anne R. ARIMA modelling of predicting COVID-19 infections. medRxiv. 2020 Apr 23;2020.04.18.20070631.
7.  Kum FV, Olayiwola S, Aloysius NM. The Impact of Ebola Virus Disease on Government Expenditure in Sierra Leone. Socio-cultural Dimensions of Emerging Infectious Diseases in Africa. 2019 Mar 20;75–90.
8. Christodoulos C, Michalakelis C, Varoutas D. Forecasting with limited data: Combining ARIMA and diffusion models. Technological Forecasting and Social Change. 2010 May 1;77(4):558–65.

Get started!

• https://medium.com/@danhhuynh12/what-simple-model-could-we-use-to-forecast-covid-19-1f1df21fe8c1
• https://towardsdatascience.com/forecasting-covid-19-cases-in-india-c1c410cfc730